When ChatGPT 3.5 came out, I heard two kinds of reactions. A friend told how impressed he was, and how it was better than several (human) interns he had in his work. Members of my family were alarmed, wondering if this was the start of an AI takeover.
In both cases, I responded that while indeed impressive, the technology was horribly inefficient. That should temper both our admiration and fear.
But am I correct? Is the technology really "horribly" inefficient? And if so, what can be done to improve it?
Short answer - Yes, much of AI technology (including artificial neural networks) is very inefficient, and the trend is not good. But there is already a lot of work trying to address the problem.
How Expensive is AI?
Most analyses of AI computing (including networking) costs focus on model training (or building) cost. Studies conclude that this cost has been growing exponentially in recent years, at a rate that has jumped since 2017 or so. For instance, the Center for Security and Emerging Technology (CSET) study, AI and Compute: How Much Longer Can Computing Power Drive Artificial Intelligence Progress?, indicates that the compute resources used by AI models have doubled every 3.4 months since the release of AlexNet (a convoluted neural network) in 2012, as compared with a doubling time of 2 years before then:

The above charts are logarithmic scale. Note how the slope dramatically increases in the last decade. The charts calculate petaFLOPS-days. The latest Green500 benchmark has the top supercomputer boasting power performance of ~65 GFlops per watt. A petaFLOP would then consume 65 MW, so the largest models in the above charts at 2.5 petaFLOPS would consume 162.5 MW. Assuming an average of 750 watts per household (actual usage varies a lot, and is driven a lot by use of air conditioning), that is the amount needed to provide energy to about 215,000 households.
Whether this is a lot or not so much for what we're getting, is up to debate. The trends are not good, however, as much (but not all, as will be discussed below) of AI progress is driven by scaling compute. The Center for Security and Emerging Technology (CSET) study, AI and Compute: How Much Longer Can Computing Power Drive Artificial Intelligence Progress?, includes the following scary projection:
Obviously, we are not going to spend our entire (much less more) GDP on training AI models. And projection is a risky business. But it does appear clear that we can't just keep increasing the data, parameters and compute resources in order to train ever more effective models.
We may also be reaching diminishing returns. In THE COMPUTATIONAL LIMITS OF DEEP LEARNING, an interesting chart shows how much additional compute has been required to reduce the error rate in image classification:
Getting the error rate down from 30% to 15% took 10000x as much compute. This is not a good slope. As the abstract of THE COMPUTATIONAL LIMITS OF DEEP LEARNING states:
Deep learning’s recent history has been one of achievement: from triumphing over humans in the game
of Go to world-leading performance in image classification, voice recognition, translation, and other
tasks. But this progress has come with a voracious appetite for computing power. This article catalogs
the extent of this dependency, showing that progress across a wide variety of applications is strongly
reliant on increases in computing power. Extrapolating forward this reliance reveals that progress
along current lines is rapidly becoming economically, technically, and environmentally unsustainable.
Thus, continued progress in these applications will require dramatically more computationallyefficient methods, which will either have to come from changes to deep learning or from moving to
other machine learning methods.
Another nice look is the following chart from the analysis Compute and Energy Consumption Trends inDeep Learning Inference:
Note how progress in accuracy has flattend out.
All this is the approximate power to train the large model. Using the model requires powering inference. While a single inference may be very inexpensive, if millions (billions) of inferences are being made (both interactively and automatically by smart devices), the aggregate cost can get very expensive. The last study, Compute and Energy Consumption Trends in Deep Learning Inference, address this. While it also finds concerning trends for state-of-the-art (SOTA) models, by moving the focus from the first implementation of a breakthrough towards the consolidated version of the techniques one or two years later, the analysis concludes that the trend is not so worrying:

The dash line shows the worrying high slope upwards for the most accurate, SOTA models. But the solid line, for all models, is much flatter. And the accuracy of those models is still quite good - much better than earlier models that use the same or more energy, and not all that behind the SOTA models. As the analysis concludes (emphasis added by me):
Our findings are very different from the unbridled exponential growth that is usually reported when
just looking at the number of parameters of new deep learning models. When we focus on inference costs of these networks, the
energy that is associated is not growing so fast, because of several factors that partially compensate
the growth, such as algorithmic improvements, hardware specialisation and hardware consumption
efficiency. The gap gets closer when we analyse those models that settle, i.e., those models whose
implementation become very popular one or two years after the breakthrough algorithm was introduced. These general-use models can achieve systematic growth in performance at an almost
constant energy consumption. The main conclusion is that even if the energy used by AI were kept
constant, the improvement in performance could be sustained with algorithmic improvements and
fast increase in the number of parameters.
The caveat from the analysis, as noted in the paper: "This conclusion has an important limitation. It assumes a constant multiplicative factor. As more
and more devices use AI (locally or remotely) the energy consumption can escalate just by means of
increased penetration".
The cautious conclusion, then, is I think that we need to find more efficient approaches, both for training cost and to prepare for hugely increased use of AI inference in future.
What is Being Done?
There are several approaches under investigation to address AI model efficiency, both in training and inference. Some tinker with the current algorithms, others are entirely new algorithmic approaches, while others involve entirely new computational hardware.
Going from least impact to most impact, some of the approaches are:
- Sparse Networks
- Mixture-of-Experts (MOE)
- Hyperdimensional Computing
- Neuromorphic Computing
- Optical Computing
- Quantum AI
The following are just very brief summaries. If interested, I encourage you to read the source papers for much much more detail.
Sparse Networks
The idea with sparse neworks is to find a sparse neural network configuration that performs (is as accurate, etc.) as a more usual dense network, but being sparse can train and infer much faster. The issue is how to find a sparse configuration without first generating the dense counterpar. Otherwise, training cost is increased, not decreased.
In
Sparse Networks from Scratch:Faster Training without Losing Performance, Tim Dettmers & Luke Zettlemoyer of the University of Washington propose an algorithm for generating a sparse neural network with a single training run that can match the accuracy of dense networks. They call their algorithm
sparse momentum, "which uses the
exponentially smoothed gradient of network weights (momentum) as a measure of persistent errors to
identify which layers are most efficient at reducing the error and which missing connections between
neurons would reduce the error the most". The network can then be built up using only those connections that reduce the error the most. Their test results show a speedup of 2.74x to 5.61x depending on the dense model being compared.
These speedups are nice, but nowhere near enough to address the exponential increase in compute that will be used by existing models. As the paper points out, advances in sparse convolution and matrix algorithms may provide further improvements.
Mixture-of-Experts (MOE)
The computations are routed by the Gating Network to a subset (in extreme, only one) of "experts" (subnetworks specializing in processing ceretain parameters). "The gating decisions may be binary or sparse and continuous, stochastic or deterministic.
Various forms of reinforcement learning and back-propagation are proposed for trarining the gating
decisions." The expert subset can achieve comparable accuracy to an entire network layer, leading to a sparser network and more efficient computation.
This result is significant, but the tests were run on relatively small models - ~1 million parameters per expert, with up to 4096 experts (~4 billion parameters total). The newest models are using much more - GPT 3.5 used 175 billion parameters, and GPT 4 is thought to have used 220 billion per model combined over 8 models for a total of 1.75 trillion!).
At theses scales, the major issue with this approach becomes the added commmunication cost of adding an additional MOE sublayer. Additional issues seen include the complexity of the routing algorithm used by the Gating Network, and increased model instability (small input changes leading to large output changes) when using sparse MOE models.
- simplified routing algorthm - use of a consolidated differentiable load balancing loss function
- routing to only 1 expert - reduces communication
- selective precision - float32 used only within the router, providing the stability of higher precision where needed but reducing overhead by broadcasting lower precision
The dense feed
forward network (FFN) layer present in the standard Transformer is replaced with a sparse Switch
FFN layer (light blue). The layer operates independently on the tokens in the
sequence.
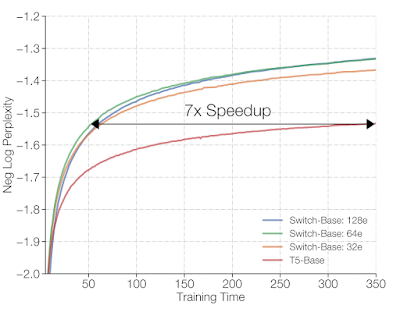
Results of tests with up to almot 15 billion parameters show much higher efficiency with the sparse Switch Transformer as compared with a dense model:
On a time basis, training is sped up 7x:
With future work, it seems reasonable to expect an order of magnitude improvement over existing dense models.
Hyperdimensional Computing
HDC [HyperDimensional Computing] maps data points (raw samples or extracted input features) in the
input space to random high-dimensional vectors, called sample hypervectors. Then, the sample hypervectors that belong to the same
class are combined linearly to obtain ensemble class hypervectors,
called class encoders. During inference, the input data is used to
generate a query hypervector (𝑄) in the same way as the sample hypervectors. The classifier simply finds the closest class hypervector
to 𝑄, generally using
cosine similarity or the
Hamming distance.
The approach has several significant consequences:
- Operations are simple sparse vector operations (addition, multiplication, permutation), and so are favorable for smaller hardware and more efficient performance on high level harddware.
- Wide, sparce data representation is resilient to noise.
- Inference based on closeness to class encoder provides robustness to inexactness and small differences in input.
Indeed, some feel hyperdimensional computing models the actual human brain!
There are practical problems, however, mostly due to the number of dimensions required to ensure orthogonality of distinct samples. Usually ~10,000 dimensions are required. This negates some of the operational efficiency, and has memory use implications.
Research is actively trying to address this problem.
Hypervector Design for Efficient Hyperdimensional Computing on Edge Devices encodes input as hypervectors not randomly with all the same high dimension, but as an optimization problem that finds the optimal number of dimensions that both maximizes the difference (orthogonality) between distinct inputs and minimizes the similarity between distinct class encoders. For several problem spaces, the study achieved from 32x to 128x reduction in dimensions as compared to the usual ~10,000, with little or no loss in accuracy:
Note: SVM is a classical support vector machine model for comparison. The data sets are the Parkinsons Disease challenge (PD), EEG error related potentials (EEG ERP), human activity recognition (HAR), and cardiotocography (CTG).
Efficient Hyperdimensional Computing presents a theoretical analysis showing that under certain conditions accuracy can be maintained or even improved with far fewer dimensions, then demonstrates this with a low dimensional encoding of the MNIST dataset (handwritten digits):
All this said, hyperdimensional computing seems to have been demonstrated mostly on classification problems, and on not very large datasets (MNIST, for instance, has only 60,000 samples in its ttraining set). It is not clear how hyperdimensional computing will perform on megascale datasets in problem spaces like large language models.
The following approaches leave software and algorithms alone, and move into entirely new hardware with corresponding software. None are quite practical for real problems currently, but may offer a future path.
Neuromorphic Computing
Neuromorphic computing, first proposed by Carver Mead over 30 years ago, models computation on the physical biology of the human brain - that is, neurons connected by synapses that fire when reaching some threshold. Inherently event driven, it promises to be highly energy efficient, like the human brain itself. One survey of neuromorphic computing models and concrete hardware implementations is
A Survey on Neuromorphic Computing: Models and Hardware. It illustrates the idea of a neuromorphic computing architecture:
One concrete example is the
True North neuromorhip chip from IBM:

- Deep learning approaches such as backpropagation and stochastic gradient descent "do not map directly to SNNs [spiking neural networks] as spiking neurons do not
have differentiable activation functions (that is, many spiking neu-
rons use a threshold function, which is not directly differentiable). "
- "Algorithms that have been successful for deep learning applications
must be adapted to work with SNNs, and these adaptations
can reduce the accuracy of the SNN compared with a similar artificial neural network".
The authors conclude: "Although neuromorphic hardware is available in the research community and there have been a wide variety of algorithms proposed,
the applications have been primarily targeted towards benchmark
datasets and demonstrations. Neuromorphic computers are not
currently being used in real-world applications, and there are still
a wide variety of challenges that restrict or inhibit rapid growth in
algorithmic and application development."
There is a brighter possibility - use for inference only for models trained as usual. There have been "several efforts to
deploy a neuromorphic solution for a problem begin by training a
DNN and then performing a mapping process to convert it to an
SNN for inference purposes. Most of these approaches
have yielded near state-of-the-art performance with potential
for substantial energy reduction ... They have shown close to deep neural network accura-
cies on benchmark image classification datasets with significantly
fewer time-steps per inference". However, even here, the authors note that "algorithms that use deep learning-style training to train
SNNs often do not leverage all the inherent computational capabilities of SNNs, and using those approaches limits the capabilities
of SNNs to what traditional artificial neural networks can already
achieve ".
Finally, perhaps further research will produce breakthough. In a survey of the latest research from the
European Research Consortium for Informatics and Mathematics in April 2021, Brain Inspired Computing, Timothee Masquelier concludes that "Back-propagation Now Works in Spiking Neural Networks!" by using surrogate gradient learning to get around the non-differentialable activation functions. In the same survey, researchers at the University of Bern address the same issue using spike timings (specifically time-to-first-spike coding) - see Fast and energy-efficient neuromorphic deep learning with first-spike times, achieving SOTA accurate digit image recognition (the MNIST dataset again) with a power consumption of only 27 microjoule per image.
Optical Computing
Optical computing uses light and analog (or digital) processes, providing faster and more efficient computation than purely electronic digital computation.
Optical Computing: Status and Perspectives offers a survey of the subject.
- Forward Optical Neural Network
- Optical Reservoir Computing
- Optical Spiking Neural Network
Optical reservoir computing has been used for edge signal processing, and not deep learning, while optical spiking neural networks are neuromorphic computing (discussed already above) on optical hardware, so I won't discuss further here.
The Forward Optical Neural Network implements the forward weights using differing approaches:
- interferometers, which represent weight vectors by varying light intensity and combine interferometers to implement vector operations
- diffractors, which represent weight vectors by spatially diffracting light intensity
- spatial light modulators, which illuminates different pixels to represent vectors and combines with lenses of different types to implement vector operations
- wavelength division multiplexing, which represents vector elements using frequencies, which are then passed through resonators to impement vector operations
A diffractor and SLM architecture can look like the following:
While optical computing has been widely exploited in different
AI models, its practical application with significantly better performance than that of traditional electronic processors has still not
been demonstrated due to various challenges.
These challenges include:
- How can the nonlinear characterization be optimized in different architectures?
- How can high-speed large-scale reconfigurability be achieved on chips with low power?
- How can different
photonics devices be integrated on a single chip?
But optical computing is very fast and very low power, so work continues!
Quantum AI
Finally, let's combine two hot and hyped areas: quantum computing and artificial intelligence!
applications provides an exhaustive review of various approaches. One of the main issues is encoding input data in suitable initial quantum states, and developing the quantum algorithms (for most devices, an applicable quantum circuit).
Challenges and opportunities in quantum machine learning discusses these issues and how they may be addressed. It is still a very open question as to whether there is or will be quantum advantage in deep learning or AI, except most promisingly when the input data itself is quantum in nature.
Of course, for any real application, much more advance in quantum computing will be required.
















No comments:
Post a Comment